神經科學與資訊理論 - Part 1

November 9, 2020

Pei

筆者亦初識資訊理論(information theory)，若理解有誤也請不吝指教。本文內容大多源於〈A tutorial for information theory in neuroscience〉這篇回顧論文，此篇以較淺白方式介紹資訊理論及其於神經科學上之應用。若有興趣深入的讀者，不妨參閱經典教科書《Elements of Information Theory》[1]、交通大學陳伯寧老師開設之線上課程[2]、或其他參考資料[3]。

為何需要資訊理論？

我們常常會聽到，神經系統負責整合感官接收到的訊息，經過中樞處理後，再送往下游產生相應動作；又或者是，神經元相接形成神經網路，訊息在神經元間傳遞，大腦得以對其進行編碼、運算、儲存等等。“訊息” 等類似辭彙雖頻繁出現，但其含義也十分模糊，我們如何描述神經元攜帶了多少訊息？兩神經元是否共享了某些訊息？此類問題顯然需要一個量化訊息的方式，而資訊理論正是合適之工具。

資訊理論的優點

無需依賴對應模型(model independent)：不需先假設目標結構(如：事先假設好神經群之間的連結關係，才進行分析)，具有更廣泛的應用場景。
可同時分析不同型態的資料，包含離散型和連續型資料，也有助於分析跨尺度的交互關係(如神經元層級 vs 腦區層級)：
- 離散型資料：如有無產生動作電位、實驗動物有無產生特定行為模式
- 連續型資料：如膜電位變化、螢光強度變化、實驗動物位置或速度
可偵測線性和非線性的交互關係
可用於多變量分析
一般而言，輸出的單位皆為bits (後文會加以介紹)，因此在不同實驗結果下比較會相對直觀(但並非可以直接比較)。

資訊理論的限制

無法建構描述系統如何運作的模型：
如：分析結果得知，A與B共享了0.05 bits的資訊，但是我們無法更進一步知道A與B是否存在直接連結，即使有，也不知道是興奮性或抑制性連結。

話雖如此，仍能透過資訊理論排除不可能的模型，限縮尋找目標的範圍。

資訊熵 (Shannon Entropy)

首先，要得知訊息量多寡的方式，是這條訊息可以消除多少來自問題的不確定性(uncertainty)。

例如這個問題：今天晚餐要吃什麼？
A：都可以
B：校外好遠，在校內吃就好
C：吃小7
很明顯的，訊息量C > B > A，又A的回答不具任何訊息量。

因此，在測定訊息量之前，得先衡量出不確定性。Claude Shannon提出以資訊熵$H(X)$ (Shannon entropy)來量化不確定性，不確定性越高，熵也就越大。
(註：熵一詞源自於熱力學，用以描述系統無序的程度，資訊熵和熱力學的熵二者在定義及概念下皆具有相似性。)
(註：為何是以$H$作為代號，可參考資料[4]。)

$$H(X) = - \sum_{x \in X} P(x)\ \log_{2}P(x)$$

公式中的$X$包含了所有可能狀態的$x$。

擲一公平硬幣，正面、反面機率皆為$\frac{1}{2}$，對於 “朝上的是哪一面？” 這個問題的不確定性：

$$H(X) = - \sum_{x \in {heads,tails}} P(x)\ \log_{2}P(x) = - [\frac{1}{2} \log_2(\frac{1}{2}) + \frac{1}{2} \log_2(\frac{1}{2})] = 1$$

擲一公平硬幣的熵(不確定性)為1 bit，我們可以理解為，用1個是非題能夠得到結果，也就是說提問 “朝上的是正面嗎？” ，若為是，則朝上的是正面，若為非，則朝上的是反面。

從上述例子得知，熵具有多少bits，就代表平均需要多少個是非題來求得最終狀態。

類似前一例，改擲一有問題的硬幣，正面機率$\frac{4}{5}$、反面機率$\frac{1}{5}$，直覺來說，這枚硬幣丟出後的不確定性會比公平硬幣來得小，因為我們知道他比較有可能是正面朝上。

$$H(X) = - \sum_{x \in {heads,tails}} P(x)\ \log_{2}P(x) = - [\frac{4}{5} \log_2(\frac{4}{5}) + \frac{1}{5} \log_2(\frac{1}{5})] \approx 0.72$$

的確，熵降到了0.72，也表現出當任一狀態出現的機率較高時，不確定性下降。

只有當各個狀態出現機率皆相同時，不確定性具有最大值(如Fig. 1 熵等於1 bit之處)；反之，若某一狀態出現機率為1，其他狀態就不可能發生，此時熵值為0，沒有不確定性(如Fig. 1 兩端)。

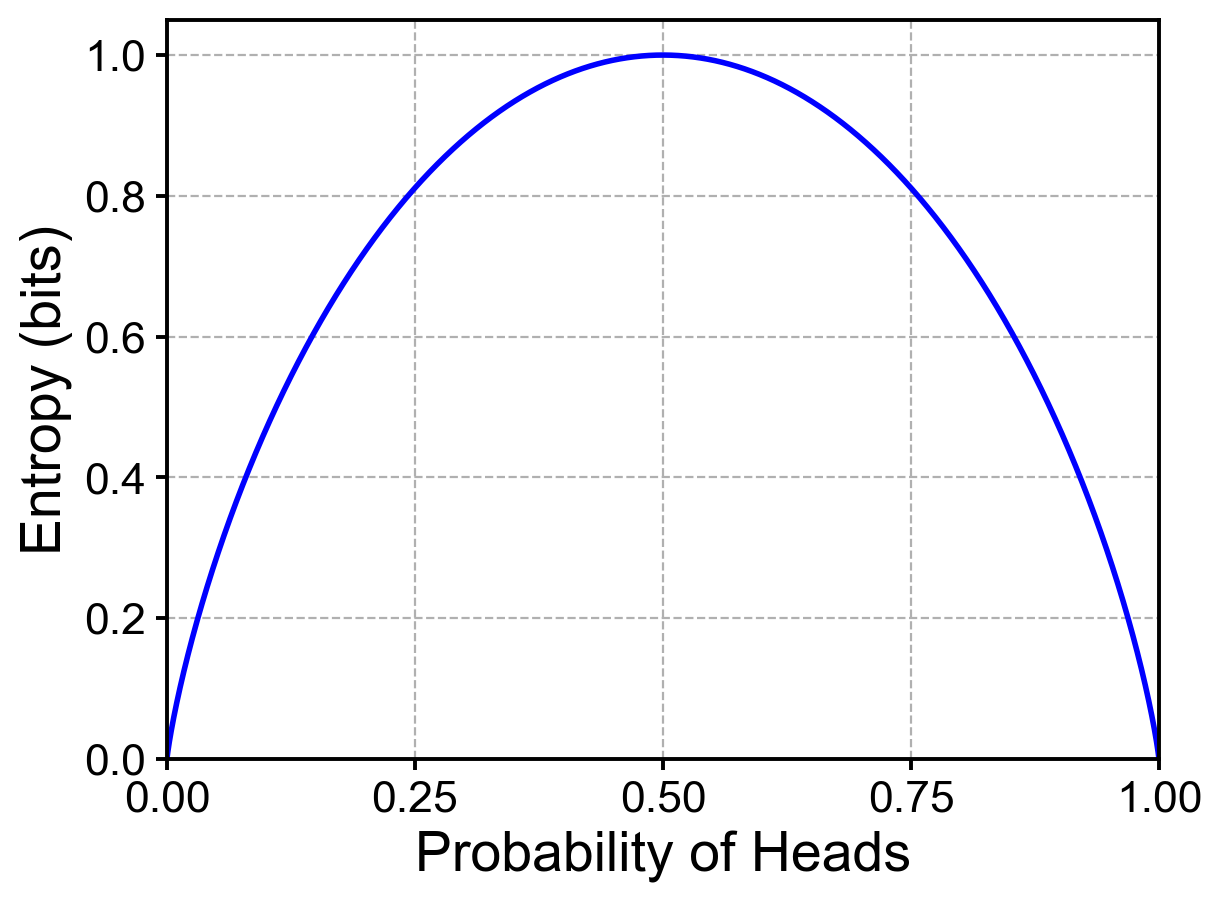
最後，資訊熵$H(X)$的公式具有幾項重要的性質：

$H(X) \ge 0$，代表熵不為負值，負的不確定性沒有解釋意義。
當任一狀態絕對會發生(機率=1)時，熵值為零，沒有不確定性。
兩獨立變量的聯合熵(joint entropy)，會等於各自的熵值相加，表現出熵的可加成性。 (此文尚未提及聯合熵，會於下一篇中介紹。)

小結

本文目前簡單介紹了資訊理論的優點和限制，並引入到資訊理論最基礎的量–熵，熵代表了不確定性，而資訊量則等同減少不確定性的程度。下一篇文中，將從一個變量增加到二個(可推廣至多變量)，並介紹聯合熵、條件熵(conditional entropy)、相互資訊(mutual information)等等在資訊理論中重要的概念。

💡

資訊代表了減少不確定性！

原始論文：

Timme, N. M. & Lapish, C. A tutorial for information theory in neuroscience. eNeuro 5, (2018) doi:10.1523/ENEURO.0052-18.2018.

參考文章：